LU DECOMPOSITION

A procedure for decomposing an  matrix  into a product of a lower triangular matrix  and an upper triangular matrix ,

LU decomposition is implemented in Mathematica as LUDecomposition[m].

Written explicitly for a  matrix, the decomposition is

This gives three types of equations

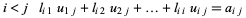
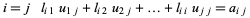
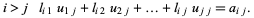
This gives 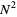 equations for  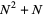unknowns (the decomposition is not unique), and can be solved using Crout's method. To solve the matrix equation

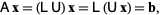
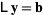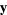first solve  for . This can be done by forward substitution

for 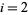, ..., 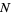. Then solve  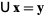for . This can be done by back substitution

for 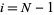, ..., 1