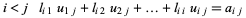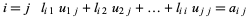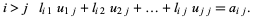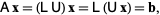Gaussian Elimination

Gauss elimination

View more presentations from luiscarlosmolina.

LU DECOMPOSITION

A procedure for decomposing an  matrix  into a product of a lower triangular matrix  and an upper triangular matrix ,

LU decomposition is implemented in Mathematica as LUDecomposition[m].

Written explicitly for a  matrix, the decomposition is

This gives three types of equations

This gives  equations for  unknowns (the decomposition is not unique), and can be solved using Crout's method. To solve the matrix equation

first solve  for . This can be done by forward substitution

for , ..., . Then solve  for . This can be done by back substitution

for , ..., 1

SYSTEMS OF LINEAR EQUATIONS: SOLVING BY SUBSTITUTION

The method of solving "by substitution" works by solving one of the equations (you choose which one) for one of the variables (you choose which one), and then plugging this back into the other equation, "substituting" for the chosen variable and solving for the other. Then you back-solve for the first variable. Here is how it works. (I'll use the same systems as were in a previous page.) Solve the following system by substitution.

The idea here is to solve one of the equations for one of the variables, and plug this into the other equation. It does not matter which equation or which variable you pick. There is no right or wrong choice; the answer will be the same, regardless. But — some choices may be better than others.


For instance, in this case, can you see that it would probably be simplest to solve the second equation for "y =", since there is already a y floating around loose in the middle there? I could solve the first equation for either variable, but I'd get fractions, and solving the second equation forx would also give me fractions. It wouldn't be "wrong" to make a different choice, but it would probably be more difficult. Being lazy, I'll solve the second equation for y:





Now I'll plug this in ("substitute it") for "y" in the first equation, and solve for x:


Now I can plug this x-value back into either equation, and solve for y. But since I already have an expression for "y =", it will be simplest to just plug into this:


Then the solution is (x, y) = (5, 4).



Warning: If I had substituted my "–4x + 24" expression into the same equation as I'd used to solve for "y =", I would have gotten a true, but useless, statement:



Twenty-four does equal twenty-four, but who cares? So when using substitution, make sure you substitute into the other equation, or you'll just be wasting your time.

GAUSSIAN ELIMINATION

Solving three-variable, three-equation linear systems is more difficult, at least initially, than solving the two-variable systems, because the computations involved are more messy. You will need to be very neat in your working, and you should plan to use lots of scratch paper. The method for solving these systems is an extension of the two-variable solving-by-addition method, so make sure you know this method well and can use it consistently correctly.

Though the method of solution is based on addition/elimination, trying to do actual addition tends to get very messy, so there is a systematized method for solving the three-or-more-variables systems. This method is called "Gaussian elimination" (with the equations ending up in what is called "row-echelon form").

Let's start simple, and work our way up to messier examples

Solve the following system of equations

It's fairly easy to see how to proceed in this case. I'll just back-substitute the z-value from the third equation into the second equation, solve the result for y, and then plug z and y into the first equation and solve the result for x.

Then the solution is (x, y, z) = (–1, 2, 3).

The reason this system was easy to solve is that the system was "triangular"; this refers to the equations having the form of a triangle, because of the lower equations containing only the later variables.

Gaussian elimination

GAUSS-JORDAN ELIMINATION

Gauss-Jordan Elimination is a variant of Gaussian Elimination. Again, we are transforming the coefficient matrix into another matrix that is much easier to solve, and the system represented by the new augmented matrix has the same solution set as the original system of linear equations. In Gauss-Jordan Elimination, the goal is to transform the coefficient matrix into a diagonal matrix, and the zeros are introduced into the matrix one column at a time. We work to eliminate the elements both above and below the diagonal element of a given column in one pass through the matrix.

The general procedure for Gauss-Jordan Elimination can be summarized in the following steps:

1. Write the augmented matrix for the system of linear equations.
2. Use elementary row operations on the augmented matrix [A|b] to transform A into diagonal form. If a zero is located on the diagonal, switch the rows until a nonzero is in that place. If you are unable to do so, stop; the system has either infinite or no solutions.
3. By dividing the diagonal element and the right-hand-side element in each row by the diagonal element in that row, make each diagonal element equal to one.

Since the matrix is representing the coefficients of the given variables in the system, the augmentation now represents the values of each of those variables. The solution to the system can now be found by inspection and no additional work is required. Consider the following example:

It is now obvious, by inspection, that the solution to this linear system is x=3, y=1, and z=2. Again, by solution, it is meant the x, y, and z required to satisfy all the equations simultaneously.

Elimination Gauss-Jordan

THE SECANT METHOD

A potential problem in implementing the Newton-Raphson method is the evaluation of the derivative. Although this is not inconvenient for polynomials and many other functions, there are certain functions whose derivatives may be extremely difficult or inconvenient to evaluate. For these cases, the derivative can be approximated by a backward finite divided difference, as in

This approximation can be substituted to yield the following it equation:

Equation is the formula for the secant method. Notice that the approach requires two

Initial estimates of x. However, because f(x) is not required to change signs between

the estimates, it is not classified as a bracketing method.

THE NEWTON·RAPHSON METHOD

Perhaps the most widely used of all root-locating formulas is the Newton-Raphson equation.

If the initial guess at the root is Xi. a tangent can be extended from the point [Xi,f(Xi)]. The point where this tangent crosses the x  axis usually represents an improved estimate of the root

The Newton-Raphson method can be derived on the basis of this geometrical interpretation (an alternative method based on the Taylor series). As in the first derivative al x is equivalent to the slope:

This can be rearranged to yield